skyplot2pano – Dokumentation
Adrian Böhlen
Dokumentation: Version 1.15 vom 24.08.2025
Applikation: Version 2.10 vom 24.08.2025
Inhalt
0 Einleitung und Zweck
skyplot2pano ist eine kommandozeilen-orientierte Anwendung, geschrieben in der Programmiersprache Awk , die sich die Funktion von SCOP.SKYPLOT zunutze macht, um Panorama-Ansichten mit Silhouetten zu berechnen sowie Sichtbarkeitsparameter abzuleiten. SCOP.SKYPLOT ist ein kleines Zusatzprogramm des Programmsystems SCOP der Technischen Universität (TU) Wien. . Ziel der Anwendung ist es, auf automatisiertem Wege ein graphisch möglichst hochwertiges Ergebnis zu erzielen und wesentliche Sichtbarkeitsparameter übersichtlich zu protokollieren.
Aus jeder Berechnung mit skyplot2pano resultieren zumindest drei Textdateien: Die prot-Datei ist das Berechnungsprotokoll, welches die angegebenen Argumente und verschiedene abgeleitete Informationen auflistet. Die extr-Datei ist eine kommagetrennte Textdatei der topographischen Extrempunkte, die mit einem Geographischen Informationssystem (GIS; z.B. ArcView, ArcGIS, QGIS...) unter Verwendung der Felder X und Y visualisiert werden kann. Die Koordinaten entsprechen dabei dem Koordinatensystem des verwendeten Höhenmodells. Die sil-Datei ist ebenfalls eine kommagetrennte Textdatei, die in gleicher Weise mit einem GIS visualisiert werden kann. Damit lässt sich die Panoramaansicht erzeugen. Die Felder X und Y kennzeichnen hier Bildkoordinaten, allerdings sind zu jedem Punkt auch die zugehörigen Lagekoordinaten gespeichert, anhand derer es z.B. möglich ist, unbekannte Gipfel eindeutig zu identifizieren. Ebenso lässt sich die Distanz jedes Punktes abfragen. Weiter ist mit dem Feld DiRel eine nach Distanz abgestufte Darstellung realisierbar.
Mittels zusätzlicher Argumente kann eine vordefinierte Namendatei in die Berechnung miteinbezogen werden, und das Panoramabild auf diese Weise mit Bergnamen und Zuordnungslinien ergänzt werden. Diese Informationen werden als DXF-Datei aufbereitet, wobei die Namenskonvention jener der prot- und sil-Datei entspricht. Bildrahmen und die Kennzeichnung des mathematischen Horizonts sind weitere Elemente dieser DXF-Datei.
1 Funktionsprinzip
1.1 Funktionalität von SCOP.SKYPLOT
Folgende Beschreibung der zugrundeliegenden Applikation ist dem Benutzerhandbuch entnommen:
In diesem Programm ist eine Lösung für die Aufgabe realisiert, aus einem Digitalen Geländemodell für einen vorgegebenen Standpunkt die Sichtbegrenzung durch die Topographie abzuleiten. Diese Problemstellung ist unter anderem in Zusammenhang mit GPS-Messungen von Bedeutung, weil damit Aussagen über die Abschattung von Satelliten getroffen werden können.
Die Ergebnisse der Berechnung werden entweder graphisch ausgegeben (Skyplot-Darstellungen) oder in numerischer Form (Datei) gespeichert.
Der Berechnung liegt ein einfacher Algorithmus zugrunde. Über den Vollkreis werden von einem vorgegebenen Standpunkt aus Profile in einem konstanten Winkelabstand gerechnet und an diese Profile jeweils die Tangente gelegt. Für jedes Profil gibt es einen Berührungspunkt zwischen Profil und Tangente, der an der Sichtbarkeitsgrenze liegt und durch seinen Abstand und Höhenunterschied vom Standpunkt beschrieben werden kann.
Durch Umrechnung in den Höhenwinkel wird die benötigte Information für die Skyplot-Darstellung gewonnen. […] Ausgegeben wird neben der tabellarischen Zusammenfassung der wichtigsten Werte eine Liste mit den Spalten Azimut, Höhenwinkel der Sichtbarkeitsgrenze und Entfernung des Grenzpunktes der Sichtbarkeit.
1.2 Ausgabe von SCOP.SKYPLOT
Relevant für die vorliegende Anwendung ist die zuletzt genannte Ausgabe. Diese ist wie folgt aufgebaut:
SKYPLOT: Extrempunkte
Date: 24.02.2024
Coordinates: 610558.00 197236.00 635.00
Model Height: 627.74
DTM File: sky.rdh
Limits: 480002.50 75002.50 810558.00 296977.50
Calculated Sector: 200.00..249.00 Grades
Angular Resolution: .10 Grades
Elevation Angles: Grades
200.0000 2.6143 38175.00
200.1000 2.5715 38150.00
200.2000 2.5672 26375.00
200.3000 2.5601 26375.00
200.4000 2.5798 26375.00
200.5000 2.6364 26250.00
etc.
Tab. 1: Output von SCOP.SKYPLOT (Auszug) mit Header und ersten Datenzeilen.
Ausgehend vom angegebenen Sektor (hier 200 – 249 gon) wird in der definierten azimutalen Auflösung (hier 0.1 gon) für jedes Azimut (Winkel zwischen geographisch Nord und aktueller Richtung) eine Berechnung durchgeführt und das Ergebnis in den drei oben genannten Spalten aufgelistet. Dabei bilden die ersten 8 Zeichen das Azimut, die nächsten 8 den Höhenwinkel und die letzten 10 Zeichen die Entfernung des Grenzpunktes der Sichtbarkeit. Die Winkeleinheit ist aus dem Header ersichtlich, standardmässig werden Grades, d.h. die Einheit gon (Neugrad) verwendet.
1.3 Auswertung der Daten für die Verortung der Punkte
1.3.1 Bestimmung der Lagekoordinaten
Hinter diesen drei Werten steckt wesentlich mehr, als man zunächst erwarten würde. Zusammen mit den Koordinaten des Standorts von dem aus die Berechnung durchgeführt wird (genannt Projektionszentrum, im Header unter «Coordinates» aufgeführt), ist es möglich, von jedem der aufgelisteten Punkte die zugehörigen Lage- und Höhenkoordinaten abzuleiten.
Zunächst muss die horizontale Distanz ermittelt werden, die auch als mathematischer Horizont bezeichnet wird, d.h. die virtuelle Gerade die in rechtem Winkel zur Lotrichtung steht, der Richtung gegen den Erdmittelpunkt hin. Dies lässt sich als vertikales Dreieck veranschaulichen, mit den beiden Eckpunkten A (Projektionszentrum) und P (Grenzpunkt der Sichtbarkeit) wobei die Entfernung der beiden der Hypothenuse entspricht. Zusammen mit dem Höhenwinkel, der meist mit dem griechischen Zeichen β bezeichnet wird, lassen sich die übrigen Parameter trigonometrisch bestimmen (siehe Abb. 1).
Mit der Entfernung in der Ebene und dem Azimut lässt sich nunmehr ein Dreieck in der Horizontalen konstruieren und damit die Lagekoordinaten des betreffenden Punktes wiederum trigonometrisch ermitteln. Je nachdem, in welcher Richtung – bezogen auf das Projektionszentrum – der Zielpunkt liegt, muss dabei unterschiedlich gerechnet werden. Abb. 2 zeigt zwei mögliche Konstellationen, wobei die Koordinaten des entfernten Punktes jeweils mit xE und yE gekennzeichnet sind. In skyplot2pano wird der Vollkreis hierzu in insgesamt 8 Sektoren zu je 50 gon unterteilt.
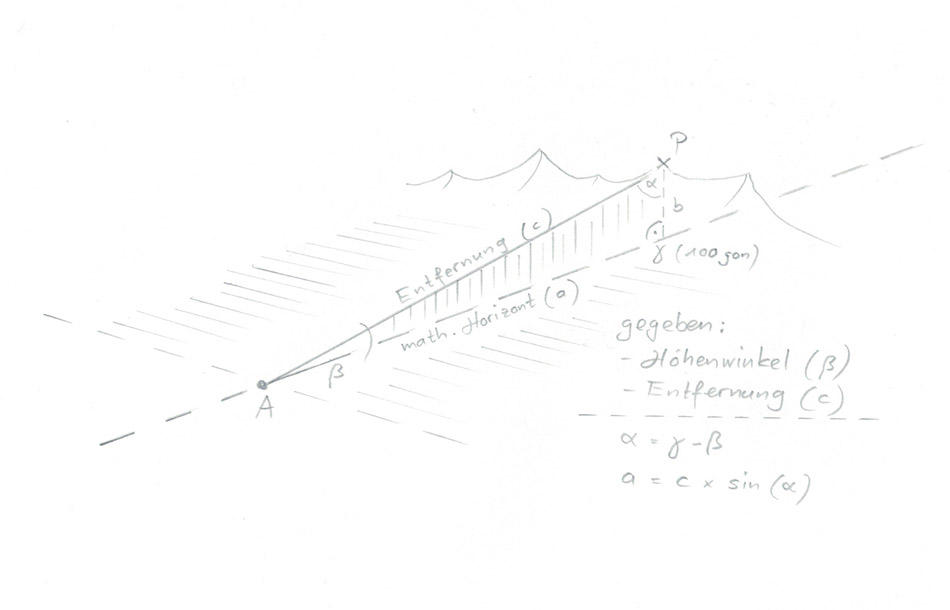
Abb. 1: Ableitung der horizontalen Distanz (Dreiecksseite a) aus Höhenwinkel β und Entfernung (Dreiecksseite c).
Eigene Zeichnung vom 02.03.2024
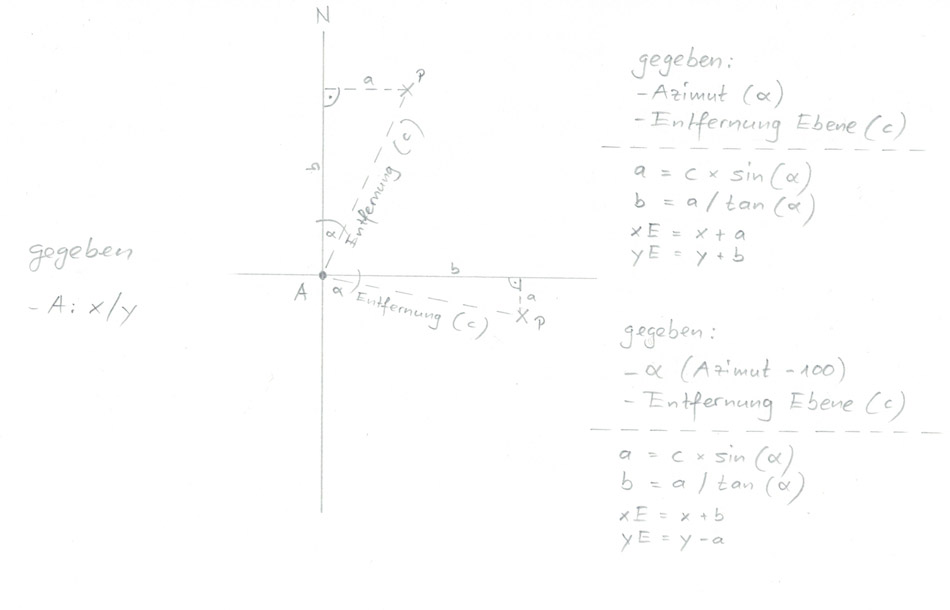
Abb. 2: Bestimmung der Lagekoordinaten eines Punktes (P; xE/yE) aus Standortkoordinaten (A; x/y), Azimut (α) und Entfernung (c).
Eigene Zeichnung vom 15.03.2024
Um die Höhe des Zielpunktes zu bestimmen genügt es nun nicht, wie man aus Abb. 1 vermuten könnte, einfach die Seitenlänge b des vertikalen Dreiecks zur Höhe des Standortes zu addieren (oder bei einem negativen Höhenwinkel zu subtrahieren), sondern es muss zusätzlich der Einfluss der Erdkrümmung und der atmosphärischen Refraktion mitberücksichtigt werden, da ansonsten grobe Fehler resultieren würden.
1.3.2 Erdkrümmung und Refraktion
Auch die höchsten Gipfel sind mit zunehmender Distanz irgendwann nicht mehr sichtbar, selbst wenn die Luft extrem klar ist und keine vorgelagerten Erhebungen die Sicht beeinträchtigen, weil sie aufgrund der Erdkrümmung früher oder später hinter dem Horizont verschwinden. Major Robert Reber, Ingenieur des Eidgenössischen Topographischen Bureaus formulierte es in seinem Aufsatz «Über Erdkrümmung und Refraktion» so: Die Erdkrümmung wirkt immer in einem negativen, d. h. für die Sichtbarkeit nachteiligen Sinne.
Dieser Parameter nimmt mit dem Quadrat der Entfernung zu. Ist der Effekt bei nahe gelegenen Objekten noch gering, so macht er sich mit zunehmender Distanz immer stärker bemerkbar. Für die Berechnung liegen verschiedene Formeln vor, die normalerweise die Erde als Kugel vereinfachen und daher von einem mittleren Radius ausgehen. Da die Erde aber in Wirklichkeit keine exakte Kugel, sondern durch die Rotation abgeplattet ist, hängt der genaue Radius vom Breitengrad ab. Für die Schweiz und die umliegenden Gebiete ergeben sich folgende Werte:
Koordinaten LV03 geographische
Stadt X / Y Koordinaten: Breite Erdradius
-----------------------------------------------------------------------
Freiburg 630060 / 316650 47° 59' 58" / 48.000° 6366.372 km
Basel 611569 / 266195 47° 32' 47" / 47.546° 6366.540 km
Bern 600000 / 200000 46° 57' 03" / 46.951° 6366.762 km
Lugano 716800 / 95984 46° 00' 19" / 46.005° 6367.114 km
Milano 737000 / 36230 45° 27' 51" / 45.464° 6367.316 km
Tab. 2: Erdradius im Bereich einiger Städte der Schweiz und des angrenzenden Auslands.
Wie man sehen kann, sind die Unterschiede aber nur gering und für die Berechnung von Sichtweiten innerhalb weniger hundert Kilometern spielt es deshalb keine Rolle, welcher dieser Werte verwendet wird. Aus diesem Grund wird der Erdradius bei skyplot2pano gerundet als 6370 km angenommen, was dem Wert entspricht, den auch SCOP standardmässig verwendet.
Hätte die Erde wie z.B. der Mond keine Atmosphäre, so könnte man es damit belassen. Da der Sehstrahl, d.h. die optische Verbindung zwischen zwei Punkten, sich aber innerhalb der Luftschicht bewegt und vor allem bei grossen Distanzen durch verschieden dichte Luftschichten hindurch, muss noch ein weiterer Parameter berücksichtigt werden; die atmosphärische Refraktion. Diese bewirkt grob gesagt eine Krümmung der Lichtstrahlen gegen die Erdoberfläche hin, oder – nochmals Robert Reber zitierend: Für gewöhnlich wird daher die Refraktion in einem positiven, für die Sichtbarkeit günstigern Sinne wirken. Gewöhnlich deshalb, weil wir es hier nicht mit einem klar festzulegenden geometrischen Wert zu tun haben, sondern sich die Eigenschaften der Atmosphäre aufgrund des Wetters (Hoch- und Tiefdruckgebiete, Inversionen…) und der Temperatur ständig verändern und dadurch auch ihre Wirkung auf die sie durchdringenden Lichtstrahlen. Als mittlerer Refraktionskoeffizient hat sich seit Carl Friedrich Gauß um 1800 der Wert 0.13 bewährt, das entspricht 13 Prozent der Erdkrümmung.
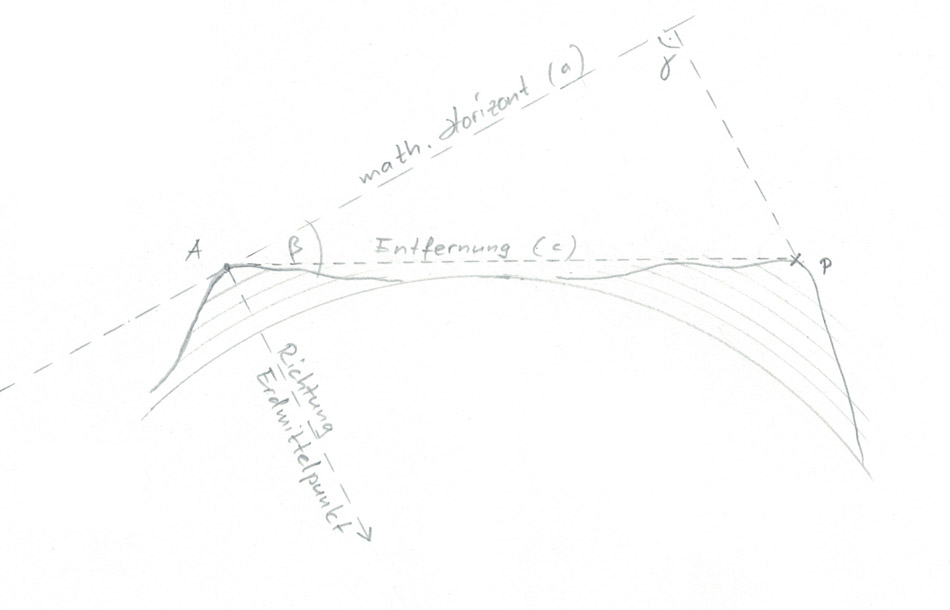
Abb. 3: Durch die Erdkrümmung verursachte Absenkung des Punktes P, der gesehen vom niedrigeren Punkt A unter dem mathematischen Horizont liegt (negativer Höhenwinkel β).
Eigene Zeichnung vom 15.03.2024
Da auch die Refraktion mit dem Quadrat der Entfernung zunimmt, wird sie zumeist mit der Erdkrümmung gemeinsam berechnet, so auch in der vorliegenden Applikation. Um also die Höhe des Zielpunktes zu bestimmen, ist gemäss der Darstellung in Abb. 1 der ermittelte Wert für die Dreiecksseite b zu der Standorthöhe zu addieren (bzw. bei einem negativen Höhenwinkel davon abzuziehen) und anschliessend die durch Erdkrümmung und Refraktion verursachte Absenkung zu addieren. So können selbst Punkte, die unter dem mathematischen Horizont liegen (negativer Höhenwinkel) in Wirklichkeit höher als der Standort gelegen sein. Abb. 3 zeigt im Seitenriss (stark übertrieben) eine solche Konstellation: Obwohl Punkt P deutlich höher als Punkt A ist, erscheint er von diesem aus betrachtet nur knapp über dem natürlichen und deutlich unter dem mathematischen Horizont.
1.3.3 Topographische Extrempunkte
Die so genannten Extrempunkte bezeichnen die am weitesten in jeder Himmelsrichtung entfernten Punkte, sowie der höchste und der entfernteste. Je nach Konstellation können mehrere Kriterien auf ein und denselben Punkt zutreffen. Zu beachten ist, dass sich die Extrempunkte immer auf den berechneten Ausschnitt beziehen. Wird beispielsweise nur die Sicht nach Süden berechnet, so entspricht der nördlichste Punkt dem Projektionszentrum und nicht etwa dem entferntesten, in nördlicher Richtung sichtbaren Punkt.
In der Protokolldatei wird zu jedem dieser Punkte auch die zuvor erläuterte Absenkung durch Erdkrümmung und Refraktion ausgewiesen, wie hier am Beispiel des Hohlohturms (Koordinaten LV03: 671940 / 396034 / 1012) ersichtlich ist:
Extrempunkt X Y Z D [km] Azi [gon] E-R [m] dH [m]
--------------------------------------------------------------------
Noerdlichster: 687535 576841 479 181.5 5.478 2249.6 -532
Oestlichster: 800997 415333 711 130.5 90.550 1163.0 -300
Suedlichster: 649006 153418 3944 243.7 206.000 4055.7 2932
Westlichster: 555173 494261 687 152.6 344.524 1590.2 -324
Hoechster: 652658 154072 4195 242.7 205.062 4023.4 3183
Entferntester: 640238 154256 4005 243.8 208.300 4060.6 2993
Tab. 3: Liste der Extrempunkte für den Standort Hohlohturm (Schwarzwald).
Erläuterungen:
- X / Y / Z: Lage und Höhenkoordinaten im gleichen rechtwinkligen Koordinatensystem wie das definierte Projektionszentrum (hier LV03 und Meter über Meer)
- D: Distanz zu diesem Punkt in km
- Azi: Azimutaler Winkel zu diesem Punkt in gon. Es gilt: Norden 0 gon, Osten 100 gon, Süden 200 gon, Westen 300 gon
- E-R: Absenkung durch Erdkrümmung und Refraktion in m
- dH: Höhendifferenz gegenüber dem Projektionszentrum. Negative Werte kennzeichnen niedrigere, positive Werte höher gelegene Punkte
Diese Daten werden zusätzlich als kommagetrennte Textdatei ausgegeben, zwecks Visualisierung in einem Geographischen Informationssystem (GIS). Die Struktur dieser Datei ist sehr einfach und beschränkt sich auf die Lagekoordinaten und die Angabe des jeweiligen Extrempunktes. Obiges Beispiel würde demnach so aussehen:
X, Y, Z, Extrempunkt
687535, 576841, 479, Noerdlichster
800997, 415333, 711, Oestlichster
649006, 153418, 3944, Suedlichster
555173, 494261, 687, Westlichster
652658, 154072, 4195, Hoechster
640238, 154256, 4005, Entferntester
Tab. 4: Output von skyplot2pano (Auszug). Kommagetrennte Textdatei für die Darstellung der topographischen Extrempunkte. Standort wie zuvor.
Ausgehend von den Spezifikationen von ArcView 3.* hat diese Datei hat die Endung *.txt. Bei der Verwendung anderer Systeme, die evtl. die Endung *.csv für solcherart stukturierte Dateien voraussetzen, muss dies manuell geändert werden. In Abschnitt 2.6 ist dokumentiert, wie der Import und die Visualisierung in einem GIS bewerkstelligt werden kann.
1.4 Auswertung der Daten für die Panoramadarstellung
1.4.1 Einleitung
Im vorherigen Kapitel wurde aufgezeigt, wie die Ausgabe von SCOP.SKYPLOT genutzt werden kann, um die Lage- und Höhenkoordinaten der betreffenden Punkte zu ermitteln. Diese Werte lassen sich aber noch in einer anderen Art auswerten, indem damit eine Panorama-Ansicht berechnet wird. Es muss dazu eine Bildgrösse festgelegt und anschliessend die einzelnen Punkte in Koordinaten dieses Bildkoordinatensystems umgerechnet werden.
1.4.2 Die Geometrie eines Panoramas
Ein Panorama, welches über die gesamte Länge das Landschaftsbild ohne Verzerrungen wiedergibt, wird durch eine Zylinderprojektion erreicht. Dazu stelle man sich vor, in der Mitte eines durchsichtigen Zylinders zu sitzen, dessen Radius dem ausgestreckten Arm entspricht. Auf diese Weise lassen sich die Konturen der Landschaft jenseits des Zylinders zeichnerisch festhalten und anschliessend das Ergebnis in Form eines langen Streifens abrollen. Egal wie lange dieser ist, das Bild bleibt verzerrungsfrei.
1.4.3 Berechnung des Panoramas
Die wichtigste Zusatzinformation hierfür ist die Bildbreite, welche als 9. Argument festgelegt werden muss. Mit dieser Angabe, sowie dem Öffnungswinkel (7. und 8. Argument) lässt sich sowohl die Ausdehnung eines gon im Bildkoordinatensystem berechnen als auch der Radius des Projektionszylinders. Dieser kann am ehesten mit der Brennweite eines Objektivs vergleichen werden, d.h. je grösser dieser Wert ist, desto grösser (und meist auch genauer) werden Details wiedergegeben.
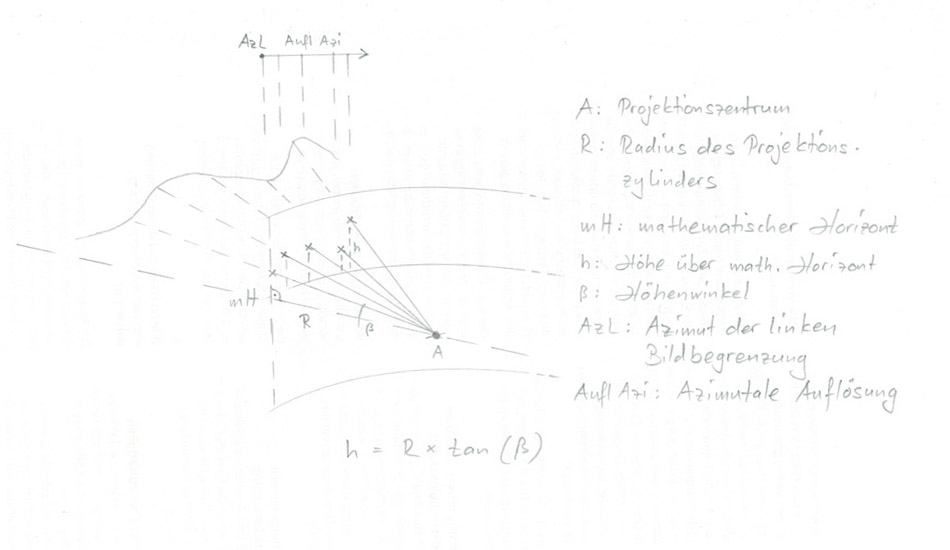
Abb. 4: Bestimmung der Höhe (h) über dem mathematischen Horizont (mH) im Bildkoordinatensystem zwecks Festlegung der Punkte, welche die Konturen der Landschaft wiedergeben.
Eigene Zeichnung vom 07.03.2024
Im Gegensatz zu einer «echten» Zylinderprojektion liegt der so genannte Hauptpunkt (Bildkoordinaten 0 / 0) hier nicht in der Bildmitte, sondern am linken Bildrand. Ausgehend von der Information, wie vielen Millimetern ein gon im Bildkoordinatensystem entspricht, wird nun ein Punkt nach dem anderen berechnet, wobei der Horizontalabstand der einzelnen Punkte (Abstand auf der X-Achse des Bildkoordinatensystems) immer genau gleich ist und der in Millimetern umgerechneten azimutalen Auflösung (6. Argument) entspricht. Der vertikale Abstand vom mathematischen Horizont (Y-Koordinate im Bildkoordinatensystem) wird trigonometrisch errechnet, indem der Radius des Projektionszylinders als Ankathete in einem rechtwinkligen Dreieck angenommen und mit dem Tangens des Höhenwinkels multipliziert wird. Abb. 4 erläutert die Zusammenhänge. Das ist wie wenn der virtuelle Panoramazeichner – um zum vorherigen Beispiel zurückzukehren – der dahinterliegenden Landschaft entsprechend, in regelmässigem Abstand einen Punkt auf den Zylinder zeichnen würde. Wie im ersten Teil erläutert, lassen sich mittels der verfügbaren Informationen die Lage- und Höhenkoordinaten ermitteln und so erhält jeder Punkt seine reale X-, Y- und Z-Koordinate als Zusatzinformation, sodass diese später im Panoramabild abgefragt werden können. Zusammen mit einigen weiteren Angaben präsentiert sich die resultierende sil-Datei am Schluss wie folgt:
X, Y, LageX, LageY, LageZ, Dist, Azi, HWink, Limit, DiRel
0.000, 10.804, 615484, 166133, 2172, 31525.0, 190.0, 3.0, 35000, 3
3.636, 9.961, 615165, 164867, 2114, 32725.0, 191.0, 2.7, 35000, 3
7.273, 11.517, 614667, 164710, 2339, 32825.0, 192.0, 3.2, 35000, 3
10.909, 11.184, 614175, 164473, 2301, 33000.0, 193.0, 3.1, 35000, 3
14.545, 11.386, 613723, 163751, 2366, 33675.0, 194.0, 3.1, 35000, 3
18.182, 10.631, 613258, 162928, 2296, 34450.0, 195.0, 2.9, 35000, 3
25.455, 7.728, 612188, 162669, 1872, 34625.0, 197.0, 2.1, 35000, 3
29.091, 7.602, 611375, 171238, 1535, 26025.0, 198.0, 2.1, 35000, 3
32.727, 7.957, 610970, 170980, 1584, 26275.0, 199.0, 2.2, 35000, 3
36.364, 9.407, 610558, 170933, 1751, 26325.0, 200.0, 2.6, 35000, 3
40.000, 10.577, 610145, 170967, 1882, 26300.0, 201.0, 2.9, 35000, 3
Tab. 5: Output von skyplot2pano (Auszug). Kommagetrennte Textdatei für die Darstellung von aus Punkten gebildeten Silhouetten.
Resultat bis und mit Version 2.0. Spätere Versionen generieren noch weitere Informationen in zusätzlichen Spalten.
Bezüglich der Dateiendung *.txt gilt dasselbe wie zuvor bei den Extrempunkten gesagte.
1.4.4 Realisierung von sichtbegrenzenden Kreten (Silhouetten)
So umgesetzt und mit einer einzigen SKYPLOT-Berechnung als Grundlage würde allerdings lediglich eine aus Punkten gebildete Linie resultieren – der natürliche Horizont. Um auch vorgelagerte Strukturen abzubilden, greift skyplot2pano zu einem Trick:
Wie dem Handbuch zu SCOP.SKYPLOT zu entnehmen ist, kann über den Parameter LIMITS ein beliebiger, durch zwei Koordinatenpaare fesgelegter Ausschnitt des Höhenmodells zur Berechnung verwendet werden. Auf diese Weise lassen sich auch nahe gelegene Erhebungen als natürlicher Horizont erzwingen. Diese Methode hat allerdings den Nachteil, dass dort, wo es keine Erhebungen im betreffenden Höhenmodell-Ausschnitt gibt, das System automatisch den Rand desselben als Sichtbegrenzung zurückliefert. Es ist daher notwendig, solche Punkte mathematisch zu ermitteln und deren Ausgabe in die Zieldatei zu unterdrücken.
Abb. 5: Ausgabe während der Berechnung von skyplot2pano
Eigener Screenshot vom 02.05.2024
Über das 12. Argument (Aufloes-Dist) wird festgelegt, in welchem Abstand der für die Berechnung verwendete Höhenmodell-Perimeter sukzessive erweitert werden soll, ausgehend von der minimalen Distanz (10. Argument), bis die maximale Distanz (11. Argument) erreicht ist. Es ist vermutlich einleuchtend, dass bei einer feinen Abstufung und dies über einen grossen Distanzbereich hinweg, eine Vielzahl einzelner Berechnungen vonnöten sind, was dann entsprechend viel Zeit in Anspruch nimmt. Der Stand der Arbeiten wird fortwährend im Kommandofenster ausgewiesen (siehe Abb. 5), wobei die Prozentwerte lediglich anhand der Anzahl Berechnungen ermittelt werden. Da jeder detektierte Geländepunkt in eine interne Liste eingetragen und folgende Berechnungen damit abgeglichen werden, um doppelte und mehrfache Punkte zu verhindern, dauern auch die einzelnen Berechnungen kontinuierlich länger. Somit ist nach 50% zwar die Hälfte der Berechnungen durchgeführt, aber noch längst nicht die Hälfte der insgesamt erforderlichen Zeit verstrichen. Letztere wird am Ende sowohl im Logfile als auch im Protokoll festgehalten.
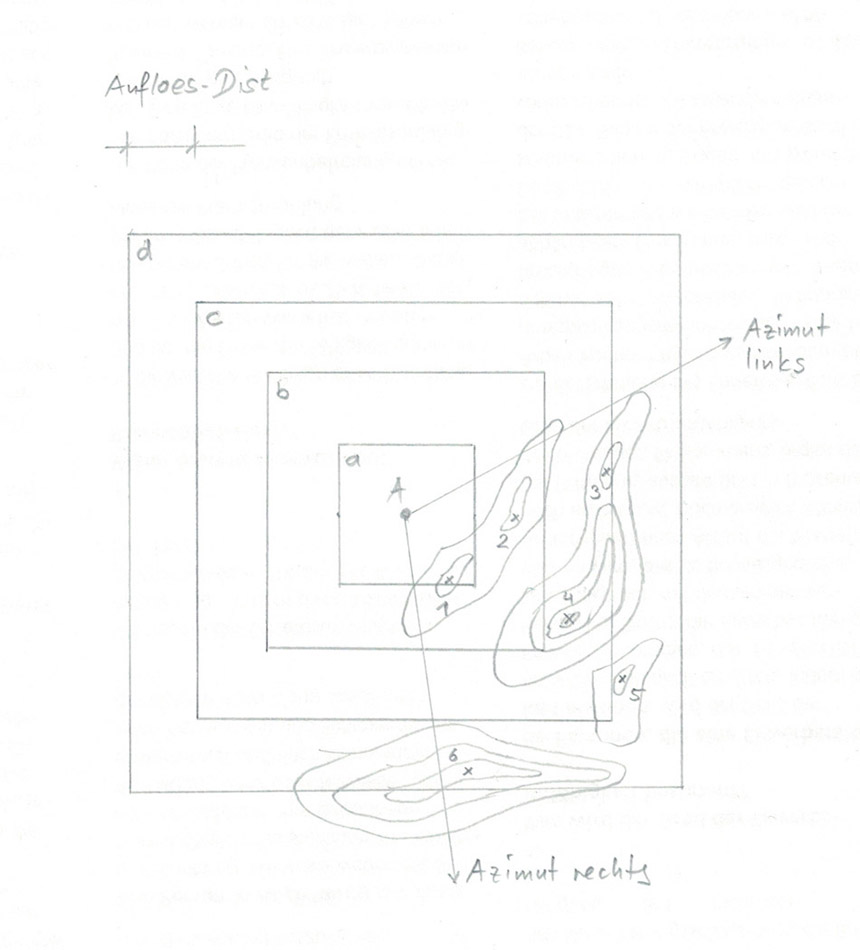
Abb. 6: Vereinfachte Darstellung von 4 aufeinander folgenden Berechnungen mit einem abstrahierten Geländemodell.
Eigene Zeichnung vom 07.03.2024
Das Funktionsprinzip ist nebenstehend in Abb. 6 erläutert: Ausgehend vom Projektionszentrum (A) wird bei einer minimalen Distanz von 0 km im Abstand, der im 12. Argument (Aufloes-Dist) fesgelegt ist, der Höhenmodell-Perimeter fortlaufend erweitert. Die nahe gelegene Erhebung 1 ist somit im ersten Durchgang (a) horizontbildend und wird als Treffer in die Ausgabedatei geschrieben. Im zweiten Durchgang (b) ist das immer noch der Fall, das System kennt diesen Punkt jedoch bereits und verwirft ihn wieder. Neu ist aber die Erhebung 2 horizontbildend, nicht jedoch der Abhang der Erhebung 4, der als Rand des Perimeters erkannt und verworfen wird. Im dritten Durchgang (c) werden die Erhebungen 3 und 4 detektiert und im vierten (d) die Erhebung 6. Die Erhebung 5 erscheint hingegen nicht in der Ausgabedatei, da sie von der Krete der Erhebungen 3 und 4 verdeckt wird.
Alternativ kann eine minimale Distanz definiert werden, die grösser als 0 ist und in diesem Fall beispielsweise der Entfernung des Perimeters c entsprechen kann. Auch dann wird die Erhebung 5 aber nicht abgebildet, da der Nahbereich in diesem Fall nicht einfach ignoriert wird. Lediglich Erhebungen, die in dieser Konstellation nicht horizontbildend sind, werden dann nicht abgebildet, hier also die Erhebungen 1 und 2.
1.5 Beschriftung des Panoramas
1.5.1 Einleitung
Im Kapitel 1.3 wurde erläutert, wie aus der Ausgabe von SCOP.SKYPLOT (Azimut, Höhenwinkel und Distanz) die Lage- und Höhenkoordinaten der einzelnen Punkte abgeleitet werden kann, und im vorherigen Kapitel 1.4 wie aus denselben Informationen die Bildkoordinaten in einem bestimmten Bildformat berechnet werden. Es ist daher naheliegend, dass es auch möglich sein muss, aus Lage- und Höhenkoordinaten eines bestimmten Punktes seine Bildkoordinaten zu ermitteln. Dazu werden die Parameter der Äusseren und der Inneren Orientierung benötigt, also die Definition des Projektionszentrums sowohl im verwendeten projizierten Koordinatensystem, als auch im Bezug auf den Bildhauptpunkt im Bildkoordinatensystem. Mit dieser Methodik können in Punktform vorliegende Namendaten in die Berechnung mit einbezogen werden, um später die auf dem Panorama sichtbaren Gipfel automatisch zu beschriften.
1.5.2 Namendatei
Für die Namendatei wird die gleiche Struktur vorausgesetzt, wie bei der Verwendung in SCOP.PER. Falls nicht vorhanden, lässt sich diese auf einfache Weise z.B. aus einer kommagetrennten Datei ableiten. Relevant für diese Anwendung sind nur die Felder Name, X-, Y- und Z-Koordinate sowie die Priorität. Das Feld Perimeter wird nicht verwendet. Die genaue Definition ist in der Dokumentation von SCOP.PER wie folgt beschrieben:
Dieser Parameter ermöglicht die Angabe des Namens jener Datei, auf der die Namensinformation vorbereitet ist. Diese Infomation besteht aus dem Namen selbst, seiner Position (X,Y,Z), der Priorität und dem Perimeter. Der Perimeter wird entweder als Radius eines Kreises oder als Umringpolygon (max. 32 Punkte X,Y) angegeben. Der Wertebereich für die Priorität liegt zwischen 1 und 99. Der Name, die Position und die Priorität müssen dem Fortran-Format (A32,3F12.2,I4) genügen; die Formatierung für den Perimeter ist frei.
Die Umsetzung weicht leicht von diesen Vorgaben ab. Durch die sich so ergebenden Puffer zwischen den einzelnen Feldern wirken sich geringfügige Verletzungen der Definition nicht direkt auf benachbarte Felder aus:
- Zeichen 1 – 32: Name
- Zeichen 35 – 44: X-Koordinate
- Zeichen 47 – 56: Y-Koordinate
- Zeichen 61 – 68: Z-Koordinate
- Zeichen 71 – 72: Priorität
Im Feld Priorität haben lediglich die Werte 98 und 99 eine besondere Bedeutung: Namen, die mit dem Wert 98 gekennzeichnet sind, werden bei der Berechnung ignoriert, und Namen mit dem Wert 99 werden auf dem Panorama immer abgebildet, egal ob sichtbar oder nicht. Auch die Distanz spielt keine Rolle; Voraussetzung ist aber, dass sie innerhalb des gewählten Sektors liegen.
Nachstehend ein Beispiel:
Dijon/Chenôve 415182.0 241952.0 370.0 99 200.
Payerne Tower 560390.0 188850.0 470.0 98 200.
Bern-Belp Tower 604802.0 195760.0 530.0 98 200.
Bourges/Neuvy-Deux-Clochers 236026.0 248988.0 411.0 99 200.
Lyon/Mont Pilat 378571.0 30730.0 1364.0 99 200.
Marseille/Grande Etoile 436596.0 -194591.0 779.0 99 200.
Aiguille du Midi 557199.0 80943.0 3842.0 99 200.
Tête de Ran 555533.0 211629.0 1422.0 46 200.
Wisle 608961.0 197193.0 674.0 41 200.
Gantrisch 600915.0 172616.0 2176.0 46 200.
Tab. 6: Selbst erstellte Namendatei in der Struktur gemäss Handbuch SCOP.PER. Die Koordinaten liegen im System CH1903 LV03 vor. Die Namen mit der Priorität 41 (Hügel) und 46 (Gipfel) werden nur dargestellt, wenn sie im abgebildeten Sektor im Sichtfeld liegen, jene mit der Priorität 98 werden ignoriert und jene mit Priorität 99 werden dargestellt, wenn sie im definierten Sektor liegen, unabhängig der Sichtbarkeit. Letztere werden in der Ausgabedatei einem separaten DXF-Layer zugewiesen (siehe Abschnitt 1.5.5).
1.5.3 Ermitteln der sichtbaren Namen
Wesentlich für das Ermitteln der sichtbaren Namen ist zum einen eine möglichst geringe azimutale Auflösung (6. Argument) und zum andern das 14 Argument (Tol) im Programmaufruf, mit welchem definiert wird, wie weit der Namenspunkt in x- und y-Richtung maximal vom ermittelten Geländepunkt entfernt sein darf, um noch abgebildet zu werden. Je kleiner dieser Wert, desto wahrscheinlicher ist es, dass der betreffende Namenspunkt auch tatsächlich sichtbar ist. Allerdings steigt dadurch auch die Gefahr, dass er nicht erscheint, wenn kein Geländepunkt in der betreffenden Distanz detektiert wird. Jeder übereinstimmende Namenspunkt wird in eine Liste eingetragen, welche bei den nächsten Punkten auf Übereinstimmung geprüft wird. Auf diese Weise wird garantiert, dass auch bei grosser Toleranz und vielen übereinstimmenden Punkten jeder Name nur einmal im Panorama erscheinen wird.
Zur Positionierung im Panorama könnten grundsätzlich einfach die Bildkoordinaten des ersten übereinstimmenden Punktes verwendet werden. Dies führt aber vor allem bei grösserer Toleranz zu einer fehlerhaften Platzierung, wie am folgenden Beispiel ersichtlich ist:
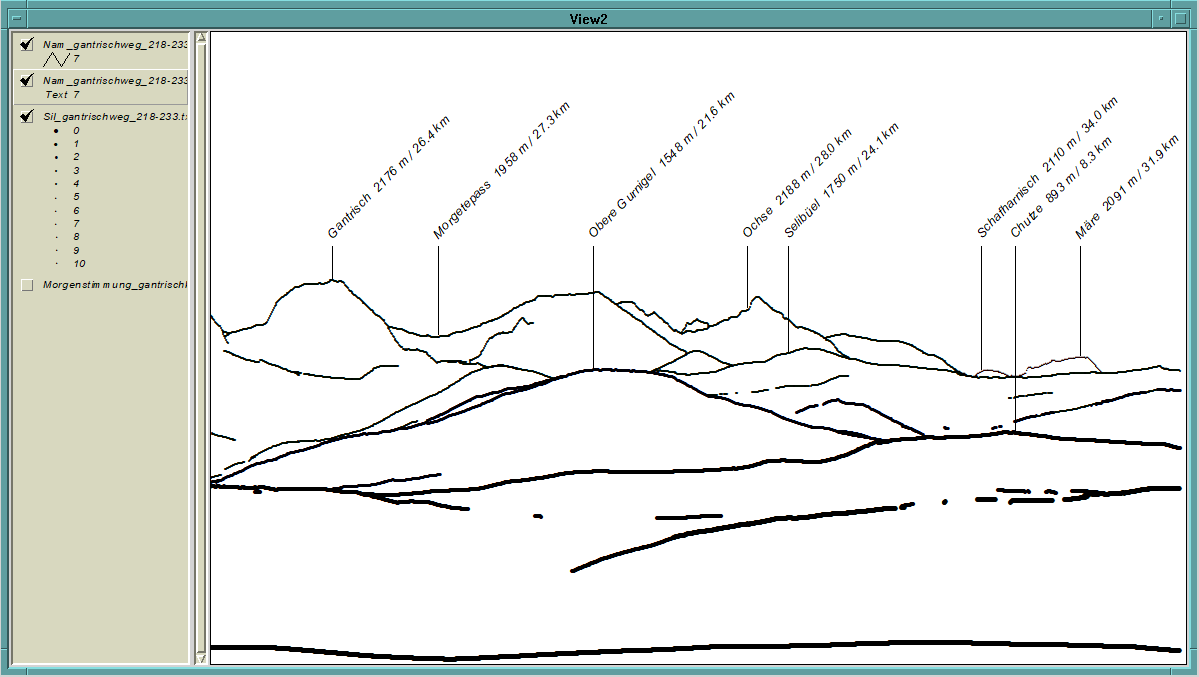
Abb. 7: Panorama-Ansicht mit Namen (Gantrischweg Richtung Gantrisch). Platzierung gemäss Geländepunkt im Toleranzbereich.
Eigener Screenshot aus ArcView vom 21.04.2024
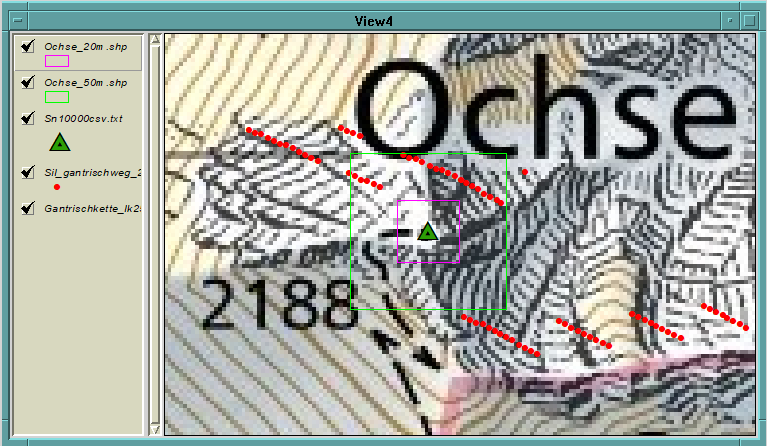
Abb. 8: Toleranzbereich 20 m und 50 m um den Namenspunkt.
Eigener Screenshot aus ArcView vom 28.04.2024
Abb. 7 zeigt das Beispiel einer Berechnung mit Namen, bei dem eine Toleranz von 50 m gewählt und die Bildkoordinaten des ersten übereinstimmenden Punktes für die Platzierung der Linie übernommen wurden. Wie sich unschwer erkennen lässt, ist das Ergebnis nicht korrekt, da einige Namen zu weit links stehen, z.B. jener des Ochse und des Selibüel. Dies deshalb, weil das Panoramabild von links nach rechts aufgebaut wird (siehe Abschnitt 1.4.3), und die im Toleranzbereich liegenden Namen schon «vor» dem Gipfelpunkt registriert werden. Bei der Reduktion der Toleranz z.B. auf 20 m würde zwar eine bessere Platzierung resultieren, allerdings steigt damit auch das Risiko, dass Namenspunkte dann nicht mehr entdeckt werden und folglich im Panorama fehlen. Warum das so ist, lässt sich anhand der Abb. 8 erkennen, die unter Zuhilfenahme der im Abschnitt 2.6.4 erläuterten Visualisierung der Punkte im Grundriss zustande gekommen ist: Das grüne Quadrat zeigt den Toleranzbereich 50 m um den betreffenden Namenspunkt, in welchem mehrere detektierte Geländepunkte (rot) liegen. Im Toleranzbereich 20 m (violettes Quadrat) ist dies nicht der Fall, daher erscheint der Namen bei dieser Parametrisierung nicht.
1.5.4 Bestimmen der Bildkoordinaten der darzustellenden Namen
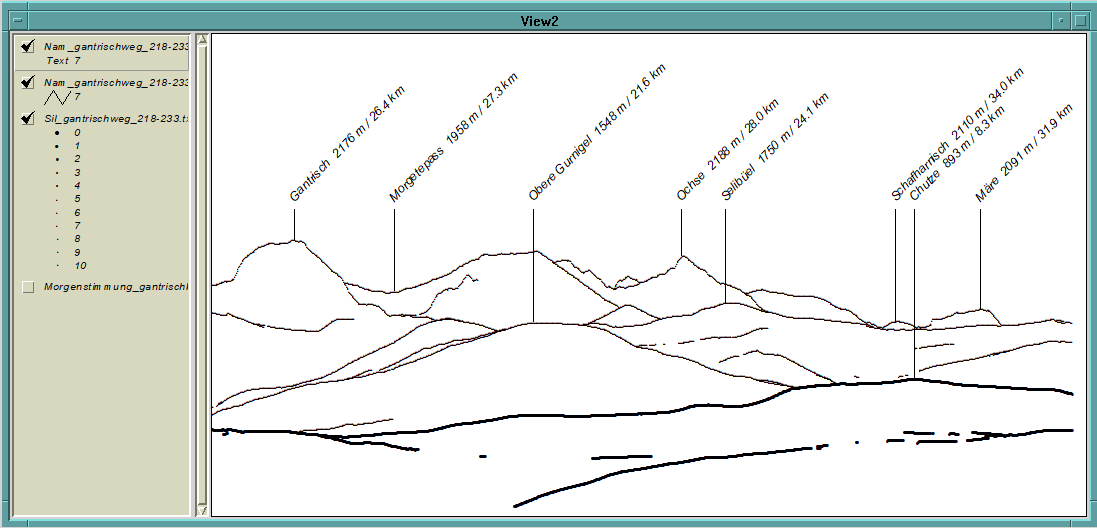
Abb. 9: Panorama-Ansicht mit korrekt platzierten Namen (Parameter wie zuvor).
Eigener Screenshot aus ArcView vom 02.05.2024
Um das Problem der Platzierung zu lösen kommt die in der Einleitung erwähnte Transformation der Lagekoordinaten in Bildkoordinaten zum Zuge. Für die als sichtbar detektierten Namenspunkte werden also nicht einfach die Bildkoordinaten der übereinstimmenden Geländepunkte verwendet, sondern die in der Namendatei (siehe Tab. 6) zu jedem Namen festgehaltenen Lagekoordinaten in Bildkoordinaten umgerechnet. Auf diese Weise wird jeder Name an der geometrisch korrekten Stelle angezeigt, wie nebenstehend in Abb. 9 ersichtlich ist. Vor allem beim Ochse und beim Selibüel sind die Unterschiede gegenüber Abb. 7 offensichtlich.
Das genaue Vorgehen ist nachfolgend für die X- und Y-Bildkoordinate separat erläutert:
Bildkoordinate X- Zunächst muss das Azimut des Namenspunktes relativ zum Projektionszentrum bestimmt werden.
Hierzu ist die in vielen Programmiersprachen (so auch in Awk) standardmässig vorhandene Funktion atan2 ideal. Sie wird mit 2 Argumenten aufgerufen, d.h. in diesem Fall der X- und Y-Koordinate des gesuchten Punktes. Abb. 10 zeigt anhand zweier Beispiele (P1 und P2), wie die Sache funktioniert: Zunächst sind die Koordinaten des Projektionszentrums (A) auf 0/0 zu reduzieren, entsprechend müssen diese von denen des zu bestimmenden Punktes abgezogen werden. Der Wert, den atan2 anschliessend als Resultat liefert, entspricht der Länge des Bogens eines Kreises mit Radius 1 zwischen Norden und der gewünschten Richtung, das so genannte Bogenmass, besser bekannt als Radiant (rad). Umgerechnet in gon wird daraus das benötigte Azimut. Zu beachten ist allerdings, dass atan2 für den Sektor Süd – Nord über West negative Werte liefert. In diesen Fällen muss das Ergebnis mit -1 mulitpliziert und von 400 (Vollkreis in gon) abgezogen werden, damit das Ergebnis den Erwartungen entspricht.
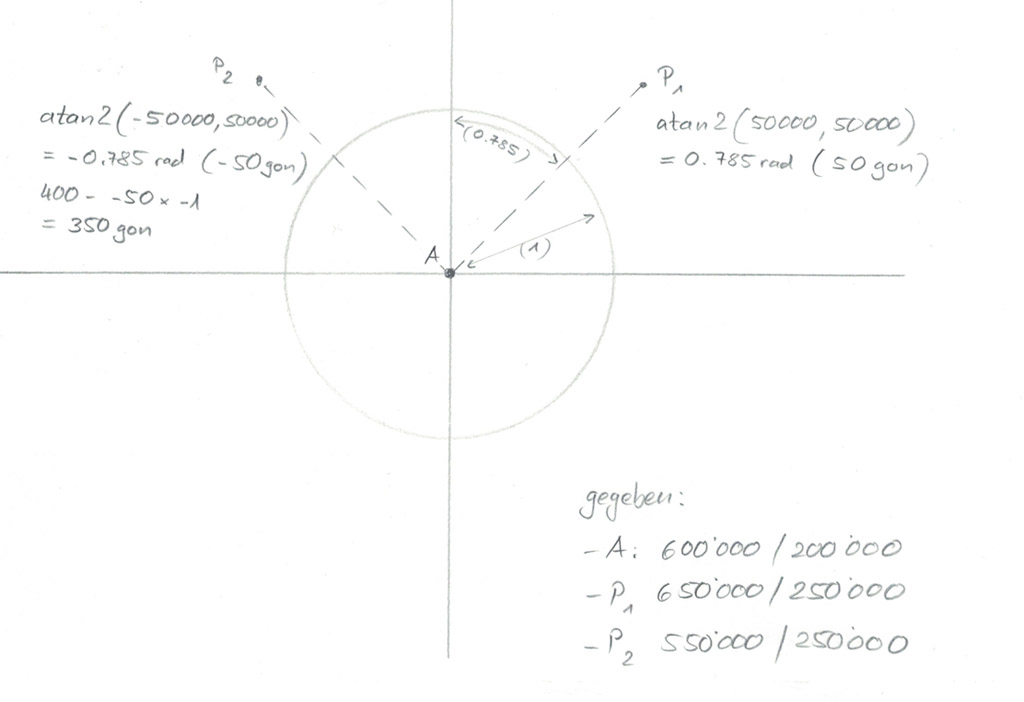
Abb. 10: Azimutbestimmung mittels atan2 anhand zweier Beispiele.
Eigene Zeichnung vom 03.05.2024 - Ausgehend der Information, wieviele mm im Bildkoordinatensystem ein Gon entspricht (siehe Abschnitt 1.4.3) kann nun die X-Bildkoordinaten dadurch gewonnen werden, indem vom Azimut des Punktes das Azimut der linken Bildbegrenzung abgezogen und das Ergebnis in mm umgerechnet wird.
- Die Y-Bildkoordinate entspricht der Höhe des Punktes. Entsprechend ist zuerst die Höhendifferenz zu ermitteln: Höhe des Namenspunktes minus Höhe des Projektionszentrums minus Absenkung durch Erdkrümmung und Refraktion (siehe Abschnitt 1.3.2). Hierfür ist vorgängig die Entfernung des betreffenden Punktes vom Projektionszentrum zu bestimmen, was mittels folgender Formel geschieht:
- Ähnlich wie in Abb. 1 wird nun ein vertikales rechtwinkliges Dreieck konstuiert, um den Höhenwinkel zu bestimmen. Dabei entspricht die zuvor ermittelte Höhendifferenz der Seite b und die Entfernung in der Ebene der Seite a.
- Wie aus dem Höhenwinkel anschliessend die Y-Bildkoordinate bestimmt wird, wurde bereits im Abschnitt 1.4.3 erklärt.
1.5.5 Bergnamen, Rahmen und mathematischer Horizont als DXF-Datei
Wie zuvor erläutert, werden während der Berechnung die Namen fortlaufend anhand ihrer Lagekoordinaten auf Übereinstimmung mit errechneten Geländepunkten geprüft und sobald eine solche gegeben ist, mit den relevanten Informationen (Name, Höhe, Distanz, X- und Y-Bildkoordinaten) in eine kommagetrennte, temporäre Textdatei geschrieben. Für die Visualisierung lässt sich diese aber nicht verwenden, weshalb am Schluss die Übersetzung in das CAD-Format DXF vorgenommen wird. DXF ist ein textbasiertes Austauschformat für CAD-Systeme, welches 1982 durch die Firma Autodesk eingeführt wurde und auch nach über 4 Jahrzehnten noch oft verwendet wird, teilweise auch im GIS-Bereich. Da es hierfür aber eigentlich nicht geeignet ist, müssen sich GIS-Nutzer mit einigen unpraktischen Eigenschaften abfinden, wie etwa der fehlenden Möglichkeit, Attribute zu verwalten. Ein grosser Vorteil ist hingegen, dass in einer einzigen DXF-Datei verschiedene Geometrietypen verwaltet werden können. Dazu gehören auch Textobjekte, so genannte Annotations.
Bei der aktuellen Umsetzung wird nur eine stark vereinfachte DXF-Struktur erzeugt, indem z.B. auf Darstellungseigenschaften (Sektion Tables) verzichtet wird. Zu jedem detektierten Punkt wird der zugehörige Name (mit Höhe in m und Entfernung in km) im Winkel von 45° oberhalb des Gipfels platziert, wobei für die Positionierung der Namen im Bild der Geländepunkt mit der höchsten Y-Bildkoordinate massgebend ist. Für die Zuweisung des Namens zum Punkt dient eine durch zwei Punkte festgelegte Linie. Ausserdem wird ein Rahmen um das Panoramabild erzeugt, wobei sich die untere Begrenzung nach dem visuell tiefsten Graphikelement richtet, welches eine Silhouette oder eine Namen-Zuordnungslinie sein kann. Die rechte und obere Begrenzung ist so gewählt, dass Namen nach Möglichkeit nicht geschnitten werden (Ausnahmen bei sehr langen Namen möglich). Bei Namen nahe des rechten Bildrandes führt dies dazu, dass die Konturlinien des Panoramas dann nicht bis zum rechten Bildrand reichen (siehe Abb. 11).
Als weiteres Element wird der mathematische Horizont rechts und links mit je einer kurzen horizontalen Linie angezeigt, kombiniert mit dem Text «Horizont» (in früheren Versionen nur «H»). Dieser müsste sich normalerweise innerhalb des Bildes befinden. Liegen allerdings alle abgebildeten Punkte entweder über oder unter dem mathematischen Horizont, so erscheint diese Markierung ausserhalb des Bildes (siehe Abb. 12).

Abb. 11: Panorama-Ansicht mit Namen bis fast zum rechten Bildrand (Hohe Möhr Richtung Alpen). Der Rahmen wird daher automatisch nach rechts erweitert.
Eigener Screenshot aus ArcView vom 18.09.2024
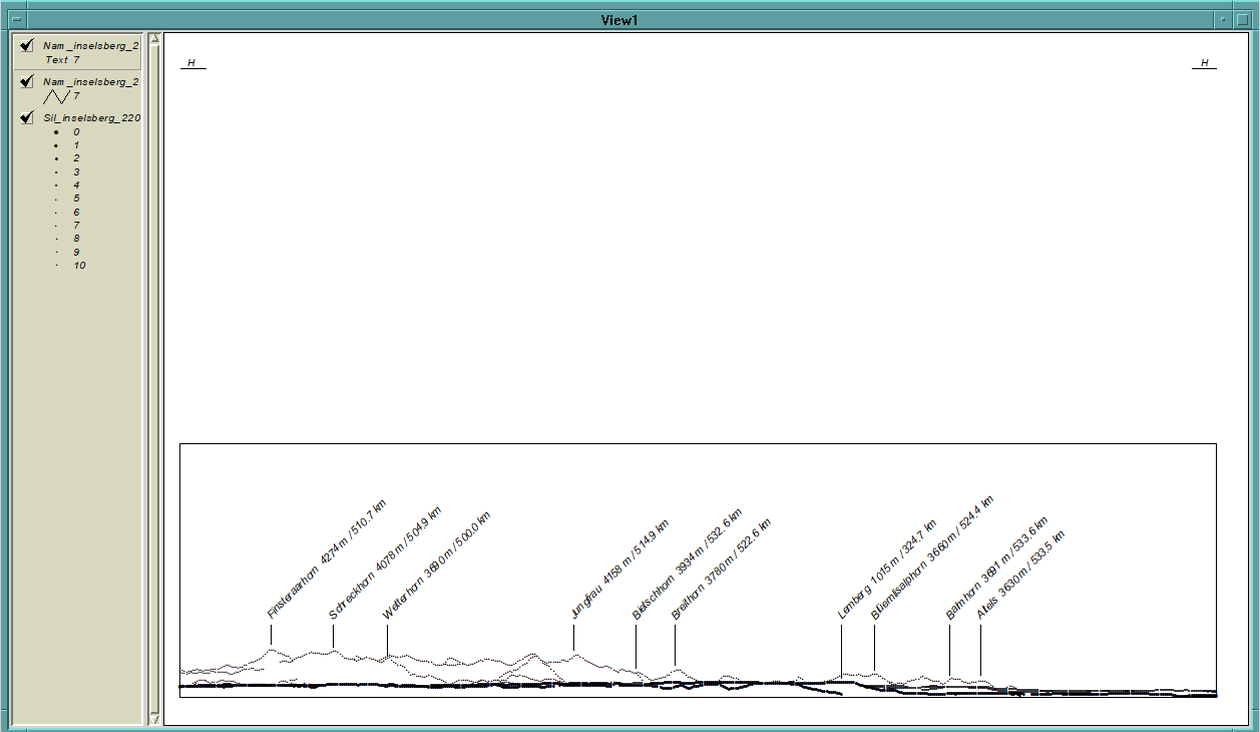
Abb. 12: Panorama-Ansicht aus sehr grosser Höhe (Großer Inselsberg plus 8000 m Richtung Alpen). Daher liegen alle abgebildeten Punkte deutlich unter dem mathematischen Horizont, der entsprechend oberhalb des Bildes angezeigt wird.
Eigener Screenshot aus ArcView vom 18.09.2024
Wie erwähnt ist die Linien- und Textdarstellung nicht definiert, allerdings sind diese Informationen beim Import in ein GIS ohnehin zweitrangig, da sie meist nicht verwertet werden können. Stattdessen sind die verschiedenen Elemente folgenden DXF-Layern zugewiesen:
Line (Polyline)- ZUORDNUNGSLINIE
- ZUORDNUNGSLINIE_99
- RAHMEN
- HORIZONT
- BERGNAME
- BERGNAME_99
- HORIZONT
So lässt sich die Darstellung der einzelnen Klassen wunschgemäss manuell gestalten. Mittels einer Definition Query können ausserdem nicht darzustellende Elemente ausgeblendet werden.
2 Benutzung
2.1 Voraussetzungen
Folgende Voraussetzungen müssen erfüllt sein, damit skyplot2pano verwendet werden kann:
- Die direkt ausführbare Quelltextdatei skyplot2pano.awk sowie die Konfigurationsdateien dhm.txt und nam.txt müssen von https://github.com/ABoehlen/skyplot2pano heruntergeladen werden.
- skyplot2pano ist in der Programmiersprache Awk geschrieben, nutzt jedoch auch UNIX-Kommandos . Es kann daher nur in einer Umgebung ausgeführt werden, die diese Befehle versteht, also z.B. einem beliebigen Linux-System, oder unter Windows innerhalb Emulatoren wie Git for Windows oder Cygwin, die auch GNU Awk bereits enthalten.
- Das Programm läuft nur mit GNU Awk (Gawk) ab Version 4.0. Unter mawk läuft es nicht. Weitere Awk-Portierungen wurden nicht getestet.
- Das Programmsystem SCOP der TU Wien wird nicht benötigt, jedoch das Zusatzprogramm skyplot.exe, welches genau aus dieser einzelnen exe-Datei besteht. Der Speicherort muss in die Umgebungsvariable PATH aufgenommen worden sein. Idealerweise wird skyplot2pano.awk am gleichen Ort abgelegt.
- Es wird zumindest ein Höhenmodell im Format SCOP RDH benötigt (*.dtm oder *.rdh Datei). Dieses hybride Höhenmodellformat kann vermutlich nur mit SCOP++ aus verschiedenen gängigen Höhenmodell-Formaten (z.B. ESRI ASCII GRID) erzeugt werden. GIS-Applikationen wie ESRI ArcGIS oder Safe FME unterstützen das Format nicht.
- Der Speicherort und die Beschreibung der verwendeten Höhenmodelle muss in der Datei dhm.txt festgelegt werden.
- Der Standort (Projektionszentrum) muss innerhalb des verwendeten Höhenmodells liegen. Es ist mit SCOP.SKYPLOT nicht möglich, von einem ausserhalb liegenden Standort auf ein Höhenmodell zu blicken (im Gegensatz zu SCOP.PER).
- Soll das Panorama mit Namen ergänzt werden, ist zumindest eine in der vorgegebenen Struktur vorliegende Namendatei erforderlich. Der Speicherort und die Beschreibung müssen in der Datei nam.txt eingetragen sein. Damit das Programm korrekt starten kann, muss diese Datei vorhanden sein, auch wenn keine Namendaten existieren. Sie enthält dann einfach nur die erste Zeile mit den Feldbezeichnungen.
2.2 Konfigurationsdateien
Damit skyplot2pano weiss, auf welche Höhenmodelle und Namendateien zugegriffen werden kann, werden zwei Konfigurationsdateien benötigt, die der Benutzer selber entsprechend ausfüllen muss. Nachfolgend je ein Beispiel. Es handelt sich um kommagetrennte Dateien, wobei der Leerraum zwischen den Feldern nur der besseren Lesbarkeit dient. Darauf kann auch verzichtet werden.
dhm.txt
Kuerzel ,Pfad ,Beschreibung
alti25 ,$SCOP_ROOT/swissalti/swissalti25.dtm ,Digitales Hoehenmodell swissALTI3D (25 m Gitter)
dhm1000 ,$SCOP_ROOT/chdtedrdh/dhm1000.dtm ,Digitales Hoehenmodell DHM25 (1000 m Gitter)
euD ,$SCOP_ROOT/euroDEM/euroDEMclip.dtm ,Digitales Hoehenmodell euroDEM (60 m Gitter)
nam.txt
Kuerzel ,Pfad ,Beschreibung
sn10 ,$SCOP_ROOT/scop/util/SWNA/sn10.txt ,swissNames3D
sn200b ,$SCOP_ROOT/scop/util/SWNA/sn200b.txt ,swissTLM-Regio Names - nur Berge
sn10000 ,$SCOP_ROOT/scop/util/SWNA/sn10000.txt ,benutzerdefiniertes Namensfile
Die unter Kuerzel eingetragene Zeichenfolge wird später beim Aufruf des Programms als Argument mitgegeben. Es dürfen hierfür nur Buchstaben, Zahlen und der Unterstrich verwendet werden. Der Pfad kennzeichnet den vollen Pfad mit UNIX-Trennzeichen (/) inkl. betreffender Datei, wobei auch Umgebungsvariablen verwendet werden können. Der unter Beschreibung eingetragene Text erscheint schliesslich im Berechnungsprotokoll. Kuerzel und Beschreibung werden ferner beim Programmaufruf ohne Argumente ausgegeben.
2.3 Aufruf über die Kommandozeile
Im einfachsten Fall wird skyplot2pano einfach über die Kommandozeile aus einem beliebigen Dateiverzeichnis heraus aufgerufen. Ohne Argumente erscheint eine Übersicht, wie die Parametrisierung zu erfolgen hat. Die Werte für die insgesamt 14 Argumente müssen durch je einen Leerschlag getrennt werden und dürfen selber keine Leerzeichen enthalten. Nachfolgend ein Beispiel: Der Sektor 218 – 233 gon wird mit einer sehr feinen Auflösung von 0.01 gon abgetastet, dies für den Distanzbereich 5 – 40 km im Abstand von 0.1 km. Die resultierende Bildbreite beträgt 200 mm. Namen sollen nicht mitberücksichtigt werden (Argumente 13 und 14 sind jeweils 0).
skyplot2pano.awk 610558 197236 635 Gantrischweg alti25 0.01 218 233 200 5 40 0.1 0 0Sind die Werte gültig, wird ausgegeben, ob das Programm mit oder ohne Berechnung von Namen laufen wird, worauf die Prozessierung beginnt und der Fortschritt ausgegeben wird, wie bereits erwähnt (siehe Abb. 5). Zum Schluss wird die Berechnungsdauer ausgegeben und im Verzeichnis, aus dem der Aufruf erfolgte, sollten sich drei neue Dateien befinden (bzw. deren vier bei der Berechnung mit Namen):
- extr_Name_AziLi-AziRe.txt (z.B. extr_Gantrischweg_218-240.txt). Dies ist die kommagetrennte Textdatei für die Darstellung der topographischen Extrempunkte in einem GIS.
- prot_Name_AziLi-AziRe.txt (z.B. prot_Gantrischweg_218-240.txt). Dies ist das Berechungsprotokoll mit den eingegebenen Werten, daraus abgeleiteten Werten sowie den topographischen Extrempunkten.
- sil_Name_AziLi-AziRe.txt (z.B. sil_Gantrischweg_218-240.txt). Dies ist die kommagetrennte Textdatei für die Darstellung von aus Punkten gebildeten Silhouetten.
- nam_Name_AziLi-AziRe.dxf (z.B. nam_Gantrischweg_218-240.dxf). Dies ist die DXF-Datei, welche bei gesetztem 13. und 14. Argument die Beschriftung enthält (Details hierzu siehe Kapitel 2.6.6).
2.4 Aufruf über einen Batch
Besser als der direkte Aufruf ist die Parametrisierung über einen Batch. Hierzu ist lediglich eine Textdatei nötig, welche einen kompletten Aufruf enthält. Damit das System diese Datei als Batch erkennt, ist es sinnvoll, in der ersten Zeile den Interpreter zu spezifizieren:
#!/bin/bashMeist funktioniert es aber auch ohne, vorausgesetzt auf der Datei ist das Ausführungsrecht gesetzt. Auf diese Weise kann dieselbe Berechnung mehrmals ausgeführt werden, oder einzelne Parameter können gezielt verändert werden, ohne jedesmal alles neu eintippen zu müssen.
2.5 Auslagerung auf eine RAM-Disk
Wie im Abschnitt 1.4.4 aufgeführt, beinhaltet ein skyplot2pano-Prozess meist eine Vielzahl einzelner Berechnungen. Dabei werden innert kürzester Zeit dutzende Dateien angelegt, ausgewertet und wieder gelöscht. Aus diesem Grund ist es sinnvoll, die Berechnung auf ein virtuelles Laufwerk, eine so genannte RAM-Disk auszulagern. Dabei wird ein Teil des Memorys (RAM) dauerhaft einem virtuellen Laufwerk zugewiesen, welches dann zur Laufzeit wie ein normales Laufwerk verwendet werden kann. Da alles innerhalb des RAM geschieht, sind viele Prozesse auf diese Weise wesentlich schneller als auf einem «richtigen» Laufwerk.
Um eine solche RAM-Disk einzurichten, ist eine entsprechende Zusatzapplikation nötig. Zu diesem Zweck gibt es verschiedene Produkte, auch kostenlose, weshalb hier auf eine Empfehlung verzichtet wird. Beim Einrichten muss man sich genau überlegen, wieviel Speicher man für das virtuelle Laufwerk «opfern» will. Möglichst viel ist natürlich in Hinblick auf grosse Höhenmodell-Dateien sinnvoll, allerdings steht dieser Speicher dann für das normale RAM nicht mehr zur Verfügung, weshalb hier eine Güterabwägung vorzunehmen ist. Hat man sich völlig vertan, kann das virtuelle Laufwerk auch einfach wieder gelöscht und nochmals von vorne begonnen werden.
Um die Berechnung im virtuellen Laufwerk ausführen zu lassen, ist ebenfalls ein Batch erforderlich, der aber einige Zeilen mehr enthält, als der zuvor genannte. Nachstehend das zuvor erläuterte Beispiel entsprechend erweitert:
#!/bin/bash
dir=$(pwd)
cd /d
skyplot2pano.awk 610558 197236 635 Gantrischweg alti25 0.01 218 233 200 5 40 0.1 0 0
mv extr_* $dir
mv prot_* $dir
mv sil_* $dir
Nach der Kennzeichnung des Interpreters (bash) in der ersten Zeile wird das aktuelle Verzeichnis der Variable dir zugewiesen. Danach wird in das virtuelle Laufwerk gewechselt, welches hier über /d angesprochen wird. Anschliessend wird dort die Berechnung vorgenommen und zum Schluss die beiden resultierenden Dateien wieder ins ursprüngliche Verzeichnis geschoben, dessen Pfad ja in der Variable dir gespeichert wurde.
2.6 Anwendungsbeispiele
2.6.1 Panorama-Ansicht visualisieren
Die kommagetrennte Ausgabedatei lässt sich problemlos in einem Geographischen Informationssystem visualisieren. Die genaue Handhabung ist bei jedem System etwas anders, weshalb darauf nicht eingegangen wird. Für die nachstehenden Beispiele wurde wie bereits zuvor ESRI ArcView GIS 3.2a verwendet . Entscheidend ist die Zuweisung der richtigen Felder für die Darstellung der X- und Y-Koordinaten im Bildkoordinatensystem. Da diese bereits mit X und Y gekennzeichnet sind, sollten sie vom System normalerweise automatisch erkannt werden. Danach erscheinen die Punkte, welche die sichtbegrenzenden Kreten repräsentieren, in einer Einheitsgrösse im Kartenfenster. Mit dem Attribut DiRel (Distanz relativ) werden die Punkte je nach Konstellation in 8 – 10 Klassen unterteilt und lassen sich daher mit unterschiedlichen Grössen symbolisieren (siehe z.B. Abb. 13). So lässt sich ein realistischer Landschaftseindruck erzielen, indem nahe gelegene Formationen mit grossen, weit entfernte dagegen mit kleinen Punkten dargestellt werden. Bei einer hohen Punktdichte, wie sie bei einer sehr geringen azimutalen Auflösung resultiert, verschmelzen die Punkte zudem zu durchgehenden Linien.
Alternativ kann die Panorama-Ansicht seit Version 2.10 auch dadurch gewonnen werden, indem der Geometrietyp Point aus der DXF-Datei, die zur Speicherung der Namensinformationen erzeugt wird, geladen wird. Dies ist aber nur dann möglich, wenn bei der Berechnung des Panoramas eine Namendatei angegeben wird. Details dazu siehe Abschnitte 2.6.7 und 2.6.8.
2.6.2 Kombination mit einer Fotografie
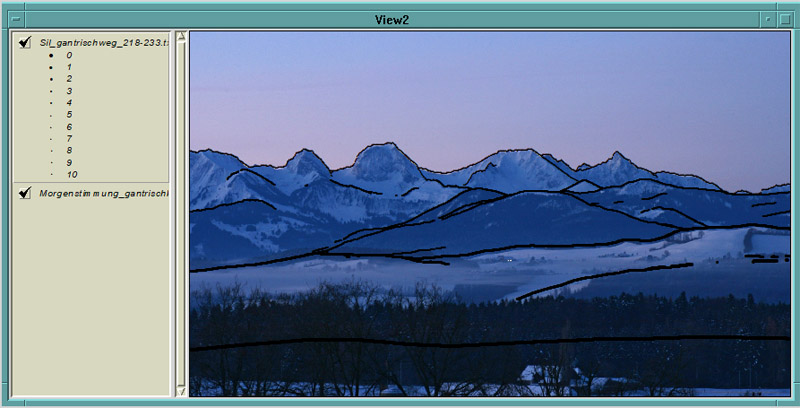
Abb. 13: Überlagerung der Silhouettendarstellung mit einer Fotografie (Gantrischweg Richtung Gantrisch).
Eigener Screenshot aus ArcView vom 09.03.2024 unter Verwendung einer eigenen Aufnahme vom 13.12.2021
Durch Festlegung zweier möglichst weit auseinander liegender Passpunkte ist es ausserdem möglich, eine Fotografie, die vom gleichen Standort aus aufgenommen wurde, auf die berechnete Geometrie einzupassen. Allerdings muss man sich dabei bewusst sein, dass eine gewöhnliche Kamera natürlich nicht mit einer Zylinderprojektion arbeitet, sondern das Bild durch das Objektiv auf eine Ebene (Sensor) projiziert wird. Je nach verwendeter Brennweite resultieren so mehr oder weniger verzerrte Aufnahmen, die dann entsprechend schlecht zu der korrekten Geometrie der Punkte passen. Dies ist besonders bei Handyaufnahmen der Fall, da die dort eingebauten Kameras nur eine sehr geringe Brennweite aufweisen. Bessere Ergebnisse gelingen mit Bildern, die mit einer Spiegelreflexkamera aufgenommen wurden. Abb. 13 zeigt ein Beispiel. Hier kam eine mittlere Teleoptik von 110 mm zum Einsatz, was eine verzerrungsarme Geometrie ermöglicht.
2.6.3 Lage der Punkte bestimmen
Wie bereits erwähnt, werden zu jedem Punkt die zugehörigen Lagekoordinaten berechnet. Mit einem entsprechenden Werkzeug (Identify o.ä.) lassen sie sich dann problemlos abfragen und z.B. mittels eines Geoportals verorten. Die Abbildungen 14 und 15 zeigen ein Beispiel unter Verwendung von https://map.geo.admin.ch. Dort lassen sich Koordinatenpaare einfach ins Suchfeld eintippen, worauf die Ansicht zur entsprechenden Stelle springt. In diesem Beispiel handelt es sich bei dem hinter dem Gemsgrat aufragenden Gipfel mit den LV03-Koordinaten 598516 171361 demnach um den Nordgipfel des 2115 m hohen Hane, der gemäss verwendetem Höhenmodell 2106 m hoch ist. Alternativ zum Abtippen können über das kombinierte Feld LageX LageY beide Koordinaten auf einmal mittels copy&paste übernommen werden, sofern das System dies zulässt.
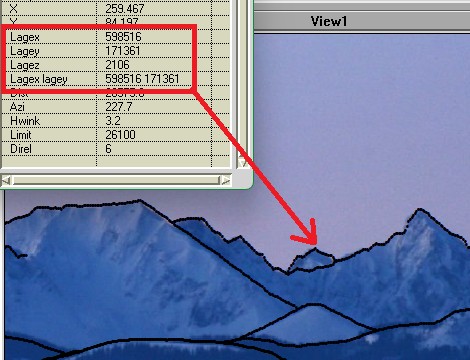
Abb. 14: Abfragen eines Punktes mit Anzeige der Lage- und Höhenkoordinaten, sowie der durch ein Leerzeichen getrennten Lagekoordinaten.
Eigener Screenshot aus ArcView vom 19.01.2025
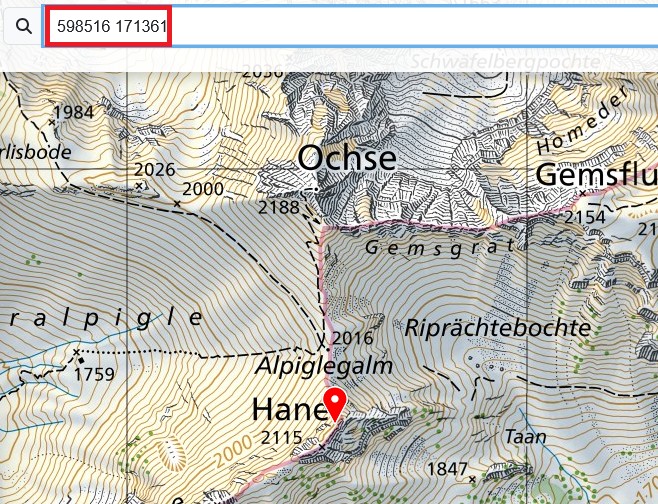
Abb. 15: Lokalisierung dieses Punktes anhand der Lagekoordinaten im Geoportal map.geo.admin.ch
Eigener Screenshot aus Firefox vom 19.01.2025
2.6.4 Anzeige im Grundriss
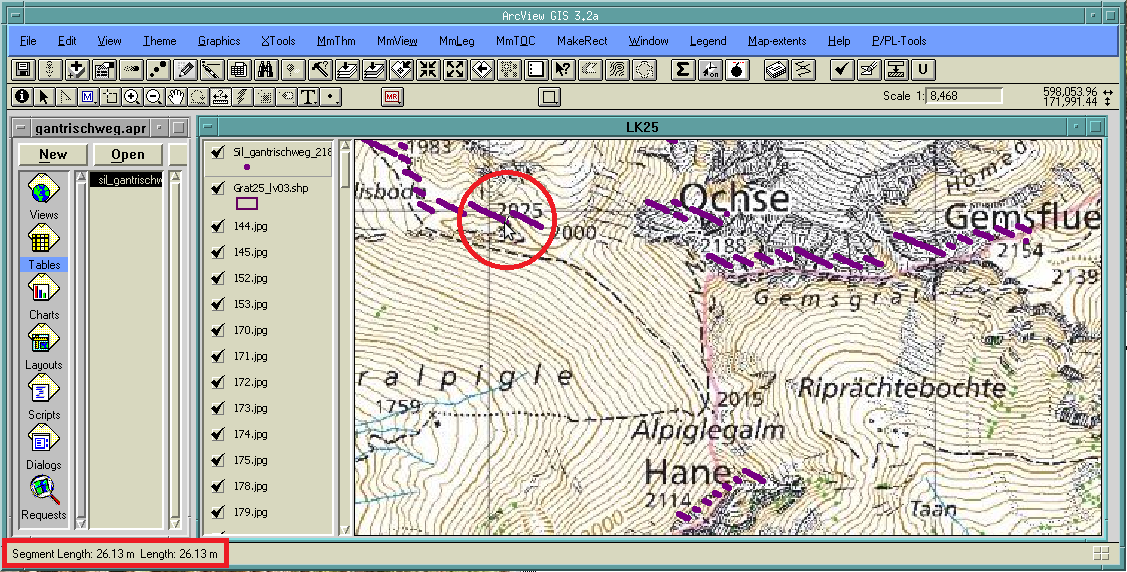
Abb. 16: Anzeige der Silhouetten im Grundriss
Eigener Screenshot aus ArcView vom 10.03.2024
Nebst der Panorama-Ansicht, welche einem Seitenriss entspricht, ist es auch möglich, sich die berechnete Datei im Grundriss anzeigen zu lassen. Das Vorgehen ist grundsätzlich identisch, mit dem Unterschied dass beim Import ins GIS als Quelle für die X-Achse im Bildkoordinatensystem das Attribut LageX und für die Y-Achse das Feld LageY festgelegt werden muss. Mit einer passenden Karte im Hintergrund lassen sich die Punkte dann gut visualisieren, allerdings darf man nicht etwa erwarten, eine Art Sichtbarkeitskarte zu erhalten. Dies ist mit der Methode, mit der SCOP.SKYPLOT arbeitet nicht möglich, da damit keine Flächen, sondern nur sichtbegrenzende Kreten erfasst werden. Wie Abb. 16 zeigt, lässt sich die Auflösung des verwendeten Höhenmodells auf diese Weise gut erkennen, da sie dem Abstand zwischen den sichtbegrenzenden Punkten in Bezug auf das Projektionszentrum entspricht; im vorliegenden Fall 25 m.
2.6.5 Visualisierung der Extrempunkte
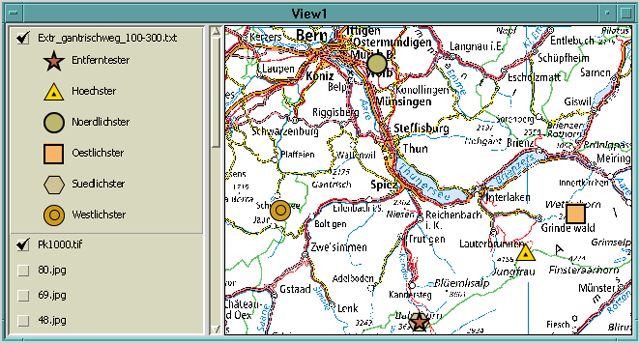
Abb. 17: Anzeige der Extrempunkte vor der Landeskarte der Schweiz 1:1 Mio.
Eigener Screenshot aus ArcView vom 21.12.2024
Ebenfalls im Grundriss können die topographischen Extrempunkte visualisiert werden. Dazu wird die bei jeder Berechnung erzeugte Datei extr_Name_AziLi-AziRe.txt verwendet. Diese ist nach demselben Prinzip wie die Datei mit den aus Punkten gebildeten Silhouetten zu laden. Die Felder X und Y kennzeichnen die Lage im gleichen Koordinatensystem wie das verwendete Höhenmodell. Über das Attribut Extrempunkt lassen sich anschliessend verschiedene Symbole für die einzelnen Punkte festlegen. Dass mehrere Extrempunkte an derselben Stelle liegen, kann dabei durchaus vorkommen, entsprechend liegen dort dann mehrere Symbole übereinander. In Abb. 17 betrifft dies z.B. den südlichsten und den entferntesten Punkt, welches in beiden Fällen das Balmhorn ist. Wie in Abschnitt 1.3.3 erläutert, beziehen sich die Extrempunkte immer auf den berechneten Sektor. In diesem Fall erfolgte die Berechnung nur von Ost über Süd nach West (100 – 300 gon), entsprechend liegt der nördlichste Punkt beim Projektionszentrum (Gantrischweg).
2.6.6 Horizontbildende Linie (Bergprofil, Profillinie)
Wie im Abschnitt 1.4.4 erläutert, wird durch die kontinuierliche Erweiterung des Höhenmodell-Perimeters vom Projektionszentrum aus eine mehr oder weniger umfassende Darstellung des sichtbaren Geländes erzielt. Manchmal ist jedoch lediglich die Wiedergabe des natürlichen Horizonts erwünscht; als gleichmässige, durchgehende Profillinie, unabhängig davon wie weit der jeweilige horizontbildende Punkt entfernt ist. Dies entspricht der eigentlichen Funktionalität von SCOP.SKYPLOT, aber eine solche Darstellung lässt sich durchaus auch mit skyplot2pano erzielen. Dazu muss man einfach das Programm dazu zwingen, nur eine einzige Berechnung durchzuführen. Für die minimale Distanz (10. Argument) und die maximale Distanz (11. Argument) kann beispielsweise fast der identische Wert verwendet werden, und zwar einer, der weiter entfernt ist als der entfernteste vom Projektionszentrum im gewünschten Sektor aus sichtbare Punkt. Zudem ist für das Intervall, mit dem der Perimeter erweitert wird (12. Argument), ein höherer Wert zu wählen, als die Differenz zwischen minimaler und maximaler Distanz. In folgendem Beispiel wurde als minimale Distanz 100, als maximale 101 und als Intervall 50 km verwendet:
skyplot2pano.awk 600377 196254 860 Gurten dhm25 0.01 190 210 200 100 101 50 0 0
Abb. 18: Profillinie (Gurten Richtung Gantrisch)
Eigener Export aus ArcView vom 31.03.2024
Um aus dem Ergebnis eine «echte» Linie zu erzielen, müssen die Punkte nach (oder je nach System bereits während) dem Import ins GIS in eine Punktdatei umgewandelt werden (Shape-, Geodatabase- oder Geopackage Format). Da die interne Reihenfolge der Punkte von links nach rechts verläuft, lassen sie sich anschliessend mit einem passenden Werkzeug mühelos in eine Linie umwandeln. Abb. 18 zeigt das aus obiger Parametrisierung erzielte Ergebnis.
Anwendungsfälle, für solche stark abstrahierten Abbildungen der Berge gibt es genügend, beispielsweise die vom Autor in Zusammenarbeit mit der Südostbahn realisierte Beschriftung der S-Bahn Züge, für die damals aber SCOP.PER verwendet wurde.
2.6.7 Erzeugen der automatischen Beschriftung
Wie im Abschnitt 1.5 erläutert, besteht die Möglichkeit, die auf dem Panorama sichtbaren Gipfel automatisch beschriften, bzw. mit Priorität 99 gekennzeichnete Namen erzwungen darstellen zu lassen. Diese Option ist allerdings noch nicht sehr ausgereift, weshalb das Ergebnis möglicherweise den Erwartungen nicht entspricht. Dazu ist als 13. Argument die als Grundlage zu verwendende Namendatei aufzuführen und als 14. Argument die Lagetoleranz in m. Welcher Wert hier ideal ist, hängt von verschiedenen Parametern ab und muss im Einzelfall durch Probieren herausgefunden werden. Bei Sichtweiten unter 100 km und einem gut aufgelösten Höhenmodell lassen sich mit 50 – 100 m im Normalfall gute Ergebnisse erzielen. Grundsätzlich ist es sehr wichtig, dass für ein gutes Resultat die azimutale Auflösung möglichst klein sein sollte, insbesondere bei grosser Distanz zu den abgebildeten Gipfeln, da es ansonsten gut möglich ist, dass die höchsten Punkte durch die Maschen fallen und so auch keine Übereinstimmung mit der Namensinformation gefunden werden kann, d.h. die betreffenden Namen dann fehlen, obwohl die Gipfel sichtbar wären. Die Toleranz sollte also bei insgesamt grossen Distanzen höher gewählt werden (100 – 500 m), was natürlich das Risiko mit sich bringt, dass mitunter «falsche», d.h. gar nicht sichtbare Namen erwischt und dann ebenfalls angezeigt werden. Allerdings muss der Toleranzwert immer kleiner sein als die Hälfte von Aufloes-Dist (12. Argument), da ansonsten ein Name bei mehreren Berechnungen als sichtbar detektiert werden kann und dann mehrfach im Panorama auftaucht.
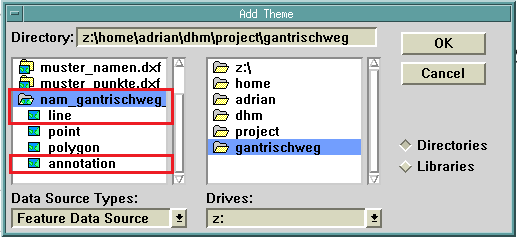
Abb. 19: Laden der Linien- und Textinformation einer DXF-Datei.
Eigener Screenshot aus ArcView vom 24.08.2025
Bei gesetztem 13. und 14. Argument wird eine Datei im DXF-Format angelegt, wobei die Namenskonvention jener der sil- und prot-Datei entspricht. Bei Verwendung einer RAM-Disk (siehe Abschnitt 2.5) darf in diesem Fall nicht vergessen werden, noch eine weitere Zeile anzufügen, die diese Datei ebenfalls von der RAM-Disk ins ursprüngliche Verzeichnis zurückschiebt.
DXF ist ein gut dokumentiertes vektorielles CAD-Format von AutoDesk, welches auch von GIS-Systemen unterstützt wird (teilweise ist wie bei ArcView 3 dazu das Aktivieren einer Extension nötig). Da eine DXF-Datei das Speichern unterschiedlicher Geometrietypen in der gleichen Datei ermöglicht, genügt es nicht, im Dateibrowser einfach das DXF auszuwählen, sondern die gewünschten Typen müssen gezielt selektiert werden. In diesem Fall sind dies Line (in einigen Systemen auch Polyline genannt) und Annotation (Text), siehe Abb. 19.
2.6.8 Darstellen der DXF-Datei
Die auf diese Weise geladene DXF-Datei erscheint in Form von 2 Ebenen in der Liste der geladenen Daten. Für die Darstellung ist es am sinnvollsten, eine Klassifizierung nach dem Attribut Layer vorzunehmen, wie in Abb. 20 gezeigt. Für den Rahmen lässt sich dann z.B. eine breite Linie definieren, für den Horizont eine feine und für die Zuordnungslinie eine strichlierte. So kann sich ein Ergebnis wie in Abb. 21 realisiert werden. Auch die Textobjekte können auf diese Weise unterschiedlich dargestellt werden, wobei sich lediglich die Schriftart und Farbe einstellen lässt, nicht jedoch die Schriftgrösse. Liegen mehrere sichtbare Namenspunkte im gleichen oder sehr ähnlichen Azimut, so überlagern sich leider die Beschriftungen. Dies lässt sich manuell nicht korrigieren, da DXF-Dateien in GIS-Systemen normalerweise nicht bearbeitet werden können. Eine Lösungsvariante ist es, die weniger wichtigen Namen zu ermitteln und in der Namendatei mit der Priorität 98 zu kennzeichnen, sodass sie bei der Berechnung ignoriert werden (siehe Abschnitt 1.5).
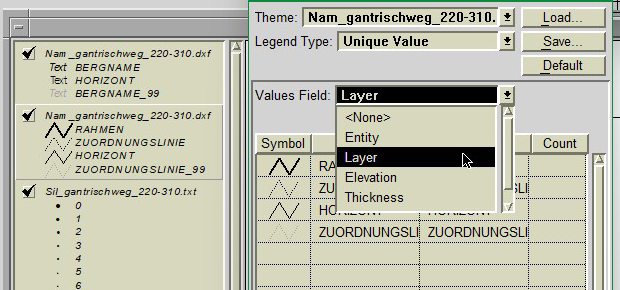
Abb. 20: Klassifizierung der DXF-Linien nach dem Attribut Layer.
Eigener Screenshot aus ArcView vom 08.06.2025
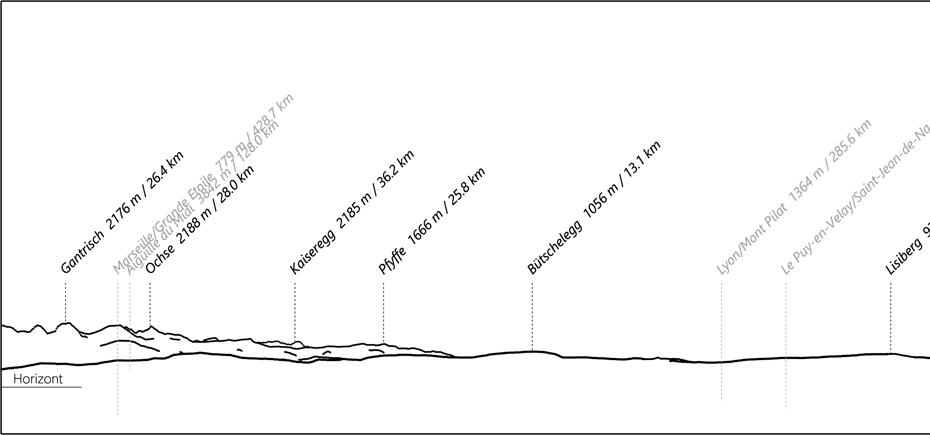
Abb. 21: Unterschiedliche Darstellung der verschiedenen Linientypen sowie der Beschriftung.
Mit der Priorität 99 gekennzeichnete Punkte (siehe Tab. 6) werden mit grauen Linien und Texten dargestellt.
Eigener Export aus ArcView vom 25.04.2025
Ab Version 2.10 werden bei Berücksichtigung eines Namensfiles, d.h. bei gesetztem 13. und 14. Attribut, zusätzlich die Silhouettenpunkte ins DXF-File geschrieben. Es ist somit nicht mehr notwendig, die Text-Silhouettendatei ins GIS zu importieren, sondern es genügt, innerhalb der DXF-Datei einfach den Typen Point auszuwählen. Um die nach Distanz abgestufte Darstellung zu erzielen, ist die DXF-Color entsprechend zu symbolisieren. Der DXF-Layer wird für die Speicherung der Lagekoordinaten verwendet. Weitere Informationen, wie z.B. das Azimut oder die Distanz können auf diese Weise aber nicht abgebildet werden. Dazu ist es weiterhin notwendig, die Textdatei zu importieren.
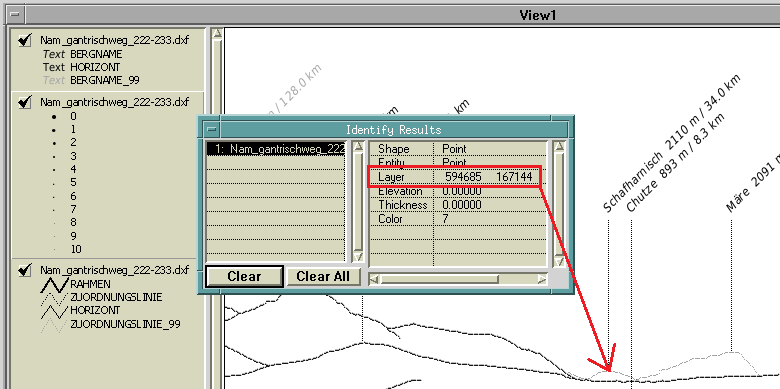
Abb. 22: Abfrage eines DXF-Silhouettenpunktes mit Anzeige der Lagekoordinaten im Attribut Layer.
Eigener Screenshot aus ArcView vom 24.08.2025
Anmerkungen, Literatur und Quellen
Da das Handbuch zu SCOP.SKYPLOT diesbezüglich keine Angaben macht, ist anzunehmen, dass dieser Wert dort ebenso gilt.